a completely firm grasp of meiosis (particularly prophase I and metaphase I) and independent assortment.
A. Complete Linkage
Two loci
that are so close that they are always inherited together.
Dihybrid
Cross: AABB x aabb = 100% AaBb
Test Cross:
AaBb x aabb. If AB and ab are linked, then progeny = 50%AB and 50% ab; no Ab
or aB
a. Basic
Principles:
- Crossing over within a region is rare (so cross-over products are rare)
- Most of the time it will not occur, so parental types will be most common
gametes produced.
b.Test Cross:
AaBb x aabb:
Suppose we observe the following phenotypic ratio in the offspring: 35 AB, 28
ab, 12 Ab, 20 aB.
AND NOW, SUPPOSE WE WANT TO ANSWER THE QUESTION: "ARE THE GENES ASSORTING INDEPENDENTLY OR ARE THEY LINKED??"
Well, that doesn't look like a 1:1:1:1 ratio like we might expect from independently assorting genes. But how different IS this ratio from what we would expect? Is it different enough to REJECT the hypothesis of independent assortment?
c. ANOTHER OVERVIEW OF HYPOTHESIS TESTING:
a. PROBLEM: How deviant do your results have to be to reject the hypothesis of independent assortment?
b. SOLUTION: Determine the probability that your results could be produced by
genes that are truly assorting independently. If this probability is really
low, your genes probably AREN'T assorting independently - they are probably
linked. (READ THIS AGAIN UNTIL IT MAKES SENSE....)
c. By analogy, suppose you have a coin and you want to know if it is perfectly
balanced. Suppose you flip it 20 times and find a 15:5 ratio of Heads:Tails.
For a perfectly balanced coin, you expect a 10:10 ratio. Suppose you can determine
that the probability that A PERFECTLY BALANCED COIN yielding a 15:5 split, just
by chance, is only 0.01%. That tells you that there is less than 1 chance in
100 that a perfectly balanced coin would deviate this much from a 10:10 expectation.
But your coin DID yield this 15:5 split. That suggests that your coin is NOT
perfectly balanced; it is behaving in a manner that is very unsualy (1/100)
for a perfectly balanced coin to behave. Of course, if you conclude that the
coin is not balanced, there is still that nagging 0.01% chance that it WAS balanced
and that your conclusion is wrong. This process is called hypothesis testing;
it is central to almost all statistical tests. The probability that chance could
produce your results is called the "alpha" level. It is also called the "type
I error rate" - defined as the probability of being wrong if you reject the
hypothesis of equality. (If you conclude that the coin is imbalanced (that your
observed results ARE NOT EQUAL TO those expected by your hypothesis), this is
the probability that your conclusion is wrong - that you've made an ERROR).
UNDERSTAND THIS LAST PARAGRAPH INSIDE AND OUT - IT WILL HELP YOU IN ALL YOUR
SCIENCE COURSES
d. DETERMINING THAT PROBABILITY FOR IND. ASSORT. GENES: The Chi-Square Test of Independence:
- Suppose you did your Dihybrid test cross and got: 35 AB, 28 ab, 12 Ab, 20 aB.
- Could these genes be assorting independently? Well, anything is possible,
but ARE THESE RESULTS LIKELY from independently assorting genes? How likely?
- Determine what you would expect if the genes assorted independently:
- For the A locus, by itself, there is a ratio of 47:48 of B:b out of 95 offspring.
- For B, there is a ratio of 55:40 of B:b.
- So, if the genes assort independently, you can predict the probability of
phenotypic combinations by multiplying the independent probabilities together.
- To find the number of individuals, you'd have to multiply this final probability
times the sample size (95). So, your expected frequencies,
under the hypothesis of independent assortment, are:
AB = 47/95 (A) x 55/95 (B) = 0.286 x 95 = 27.21 AB
Ab = 47/95 (A) x 40/95 (b) = 0.208 x 95 = 19.79 Ab
aB = 48/95 (a) x 55/95 (B) = 0.293 x 95 = 27.79 aB
ab = 48/95 (a) x 40/95 (b) = 0.213 x 95 = 20.21 ab
TOTAL = 95 offspring
e. You can calculate these in a 2 x 2 Chi-square Test of Independence Table
(also known as a contigency table) as:
(Row Total x Column Total)/ Grand Total
Compare observed vs. expected using the chi-square computation: X2 = SUM [(o-e)2/e]:
observed expected
o-e (o -e)2/e
AB 35
27.21 7.79
2.23
Ab
12
19.79 -7.79 3.07
aB
20
27.79 -7.79 2.18
ab
28
20.21 7.79
3.00
SUM = 10.48
f. Interpreting the Chi-Square Value of 10.48 - Statisticians have determined how likely particular chi-square values are, just by chance, if the events truly ARE independent. They have determined that, with 1 'degree of freedom' (what you have: (rows - 1)(columns - 1) )), a score of 3.84 will only occur 5% of the time. A score of 6.63 will only occur 1% of the time, just by chance, when two events truly ARE independent. Larger scores are progressively less likely. Your score of 10.48 signifies that truly Independently Assorting genes would ONLY yield results this deviant from what you would expect less than 1% of the time. - So, independently assorting genes are unlikely to yield your results. There is less than 1 chance in 100 that independently assorting genes would produce results that deviate this much from expectations. - The most appropriate conclusion is, then, that your genes are NOT assorting independently. You should conclude that they are linked.
HOW ARE THE ALLELES ARRANGED ON THE PARENT'S CHROMOSOMES, and
HOW FAR APART ARE THE LOCI?
1. Gene Arrangement
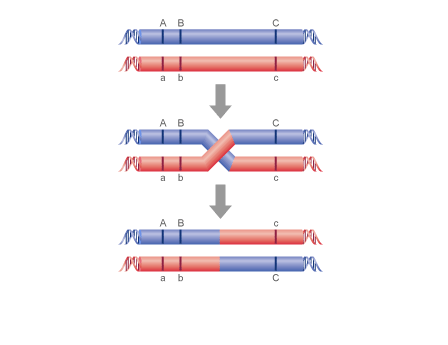
We now apply the first principle - that crossing over in a region is rare. So, the products of this rare event will be rare. So, we can identify the products of crossing over as the rarest phenotypes produced in the offspring. In this case, those are Ab and aB. These are called the recombinant types.
If crossing over is rare, then most of the time it does NOT occur. So, most of the time, the alleles are passed to the offspring in their original arrangement... and these phenotypes should be the most abundant phenotypes in the offspring. In our case, these are the AB and ab phenotypes. So, the original AaBb parent had the A and B alleles on one chromosome and the a and b alleles on the other homologous chromosome. When a cross-over occurs between these loci, the recombinant types (Ab and aB) are produced.
2. How far apart are the loci?
Well, now we apply the second principle - that the frequency of crossing over is proportional to the distance between loci. So, we measure the frequency of crossing over and can use that as a direct index of the distance between loci. So, there were 12 Ab and 20 aB offspring... for a total of 32 offspring produced by recombination events. this is 33.7% (32/95). So, we say that the genes are 33.7 map units (or centiMorgans) apart. Genes that are closer together will recombine less often... genes that are farther apart will recombine more often.
Consider these results from the following testcross:
AaBb x aabb
F1 Phenotypes:
AB 15
Ab 22
aB 29
ab 13
Conduct a chi-square tst of independence. Using the p = 0.05 level (and critical X2 of 3.64), make a conclusion about whether the genes are linked or assort independently.
If the genes are linked, map their positions in the heterozygous parent, showing which alleles are on which homolog, and determining the distance between loci.